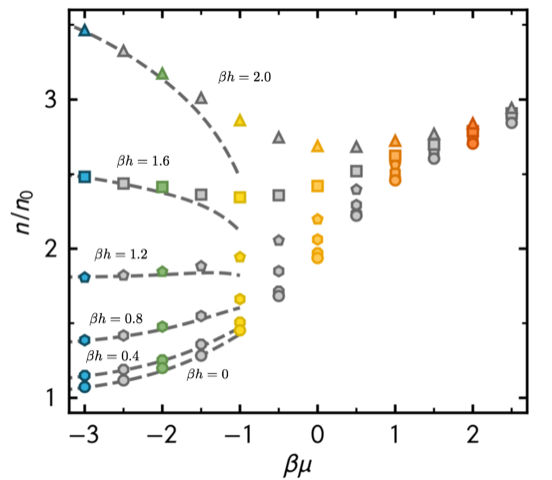
In a recent paper published in Physical Review Letters [1], UNC graduate student Andrew Loheac and his advisor Prof. Joaquín Drut tackled the long-standing problem of calculating the properties of polarized fermions in the universal regime known as the unitary Fermi gas. The figure below shows the density equation of state as a function of the chemical potential, for several polarizations. The thermodynamics of polarized fermions (nuclei, nuclear matter, cold atoms) is one of the most challenging problems in quantum physics. It suffers from a pervasive issue called the sign problem, which makes probabilities complex and has prevented Monte Carlo calculations for decades.
The recent publication [1] is the culmination of a long journey that they started in 2014. In a previous work within the same project [2], they explored the application of a variety of methods to systems that feature a sign problem due to repulsive interactions. In a follow-up publication [3], they carried out (in collaboration with Jens Braun from TU Darmstadt in Germany) the first exploration of the thermal properties of polarized fermions in one spatial dimension using a complex version of quantum Monte Carlo known as complex Langevin (CL). The successful comparison of the CL results with several other methods (such as perturbation theory and the virial expansion) paved the way for realistic systems in higher dimensions, leading to the recent Letter on the polarized unitary Fermi gas.
[1] L. Rammelmueller, A. C. Loheac, J. E. Drut, J. Braun, Phys. Rev. Lett. 121, 173001 (2018). [2] A. C. Loheac, J. E. Drut, Phys. Rev. D 95, 094502 (2017). [3] A. C. Loheac, J. E. Drut, J. Braun, Phys. Rev. D 98, 054507 (2018).